数据结构之二叉堆

概述

• 二叉堆本质上是完全二叉树，分最大堆和最小堆。
• 最大堆的任何一个父节点的值，都大于或等于它左右孩子节点的值。
• 最小堆的任何一个父节点的值，都小于或等于它左右孩子节点的值。
• 二叉堆的根节点叫做堆顶。

构建二叉堆

• 堆的插入操作是单一节点的上浮。
• 堆的删除操作是单一节点的下沉。
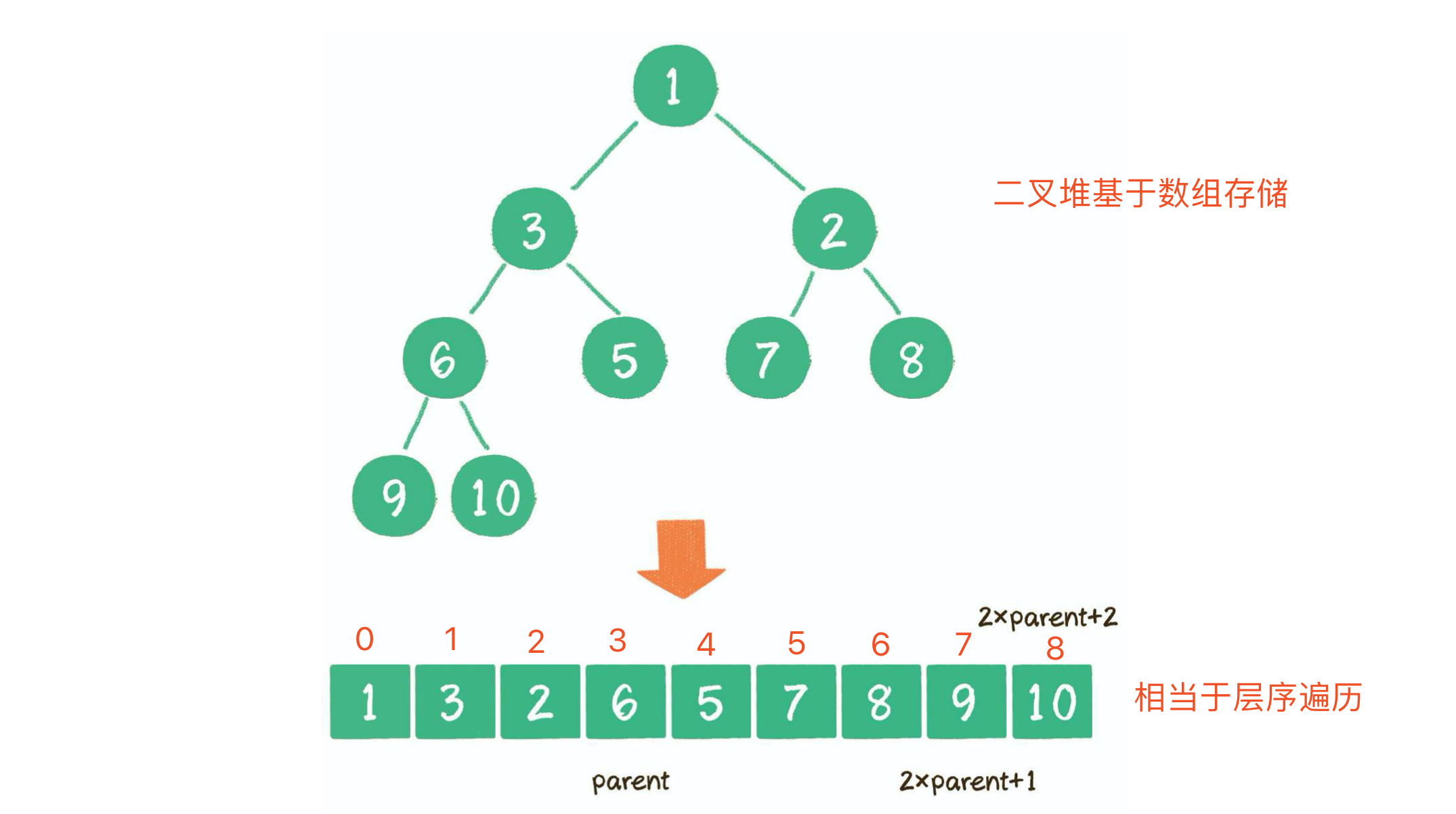
• 二叉堆的物理存储方式基于数组。

二叉堆代码实现

public class Heap {

    // 上浮调整
    public static void upAdjust(int[] array) {
        int childIndex = array.length - 1;
        int parentIndex = (childIndex-1)/2;
        int temp = array[childIndex];
        while (childIndex>0 && temp<array[parentIndex]) {
            array[childIndex] = array[parentIndex];
            childIndex = parentIndex;
            parentIndex = (parentIndex-1)/2;
        }
        array[childIndex] = temp;
    }

    // 下沉调整
    public static void downAdjust(int[] array, int parentIndex, int length) {
        int temp = array[parentIndex];
        int childIndex = 2*parentIndex+1;
        while (childIndex<length) {
            if (childIndex+1<length&&array[childIndex+1]<array[childIndex]) {
                childIndex++;
            }
            if (temp<array[childIndex]) {
                break;
            }
            array[parentIndex] = array[childIndex];
            parentIndex = childIndex;
            childIndex=2*childIndex+1;
        }
        array[parentIndex]=temp;
    }

    public static void buildHeap(int[] array) {
        // 从最后一个非叶子节点开始，依次做下沉操作
        for (int i=(array.length-2)/2; i>=0; i--) {
            downAdjust(array, i, array.length);
        }
    }

    public static void main(String[] args) {
        int[] array = new int[]{1,3,2,6,5,7,8,9,10,0};
        upAdjust(array);
        System.out.printf(Arrays.toString(array)); // 输出: [0, 1, 2, 6, 3, 7, 8, 9, 10, 5]

//        array = new int[]{7,1,3,10,5,2,8,9,6};
        array = new int[]{1,3,2,6,5,7,8,9,10,0};
        buildHeap(array);
        System.out.printf(Arrays.toString(array)); // 输出: [0, 1, 2, 6, 3, 7, 8, 9, 10, 5]
    }
}

堆排序

public class HeapSort {

    /**
     * 将数组调整为符合堆规律的结构
     * @param arr   传入需要调整的数组
     * @param parent    父结点
     * @param length    需要调整的数组长度
     */
    public static void heapAdjust(int[] arr, int parent, int length) {
        int temp = arr[parent];//先保存父结点的值，以便后续移动交换
        int child = parent * 2 + 1;//先获取到该父结点的左子结点
        while (child < length) {
            //如果存在右子结点，且右子结点大于左子结点，则选取右子结点
            if (child + 1 < length && arr[child] < arr[child + 1]) {
                child++;
            }
            //判断父结点（待插入的值）是否比子节点大
            if(temp>arr[child]){
                break;//父结点大，结束当前循环
            }else {
                /*此处类似与直接插入排序的思想*/
                arr[parent]=arr[child];//将子结点的值覆盖父节点的值
                parent=child;
                child=child *2+1;
            }
        }
        //此时已经找到合适的位置,将待插入的值插入合适的位置
        arr[parent]=temp;
    }

    /**
     *堆排序(升序)
     * @param list
     */
    public static void sort(int[] list){
        // 把无序数组构建成最大堆
        for (int i = list.length/2; i >=0 ; i--) {
            heapAdjust(list,i,list.length);
        }
        //循环删除堆顶元素
        for (int i = list.length-1; i >0; i--) {
            //将最大值list[0]与最后一个元素交换
            int temp=list[i];
            list[i]=list[0];
            list[0]=temp;
            //交换完之后，最大值已经在底层数组的末尾，然后将交换后的堆进行调整
            heapAdjust(list,0,i);//注意这里的长度已经-1了，所以堆调整不包含最后一个元素
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

TopN问题求解

题目描述

有一个 1GB 大小的文件，文件里每一行是一个词，每个词的大小不超过 16B，内存大小限制是 1MB，要求返回频数最高的 100 个词(Top 100)。

解答思路

由于内存限制，我们依然无法直接将大文件的所有词一次读到内存中。因此，同样可以采用分治策略，把一个大文件分解成多个小文件，保证每个文件的大小小于 1MB，进而直接将单个小文件读取到内存中进行处理。

思路如下

首先遍历大文件，对遍历到的每个词x，执行 hash(x) % 5000，将结果为 i 的词存放到文件 ai 中。遍历结束后，我们可以得到 5000 个小文件。每个小文件的大小为 200KB 左右。如果有的小文件大小仍然超过 1MB，则采用同样的方式继续进行分解。

接着统计每个小文件中出现频数最高的 100 个词。最简单的方式是使用 HashMap 来实现。其中 key 为词，value 为该词出现的频率。具体方法是：对于遍历到的词 x，如果在 map 中不存在，则执行 map.put(x, 1)；若存在，则执行 map.put(x, map.get(x)+1)，将该词频数加 1。

上面我们统计了每个小文件单词出现的频数。接下来，我们可以通过维护一个小顶堆来找出所有词中出现频数最高的 100 个。具体方法是：依次遍历每个小文件，构建一个小顶堆，堆大小为 100。如果遍历到的词的出现次数大于堆顶词的出现次数，则用新词替换堆顶的词，然后重新调整为小顶堆，遍历结束后，小顶堆上的词就是出现频数最高的 100 个词。

(即删除当前最小堆顶元素，留下100个)

方法总结

分而治之，进行哈希取余；
使用 HashMap 统计频数；
求解最大的 TopN 个，用小顶堆；求解最小的 TopN 个，用大顶堆。

下集预告

今日内容整理自网络。后期将会抽时间出一个实战系列。包括SpringCloud、docker、k8s、jenkins、prometheus等集开发、测试、部署、运维流程的笔记。