Java排序算法

算法 , , 评论

各种内部排序算法的比较

冒泡排序

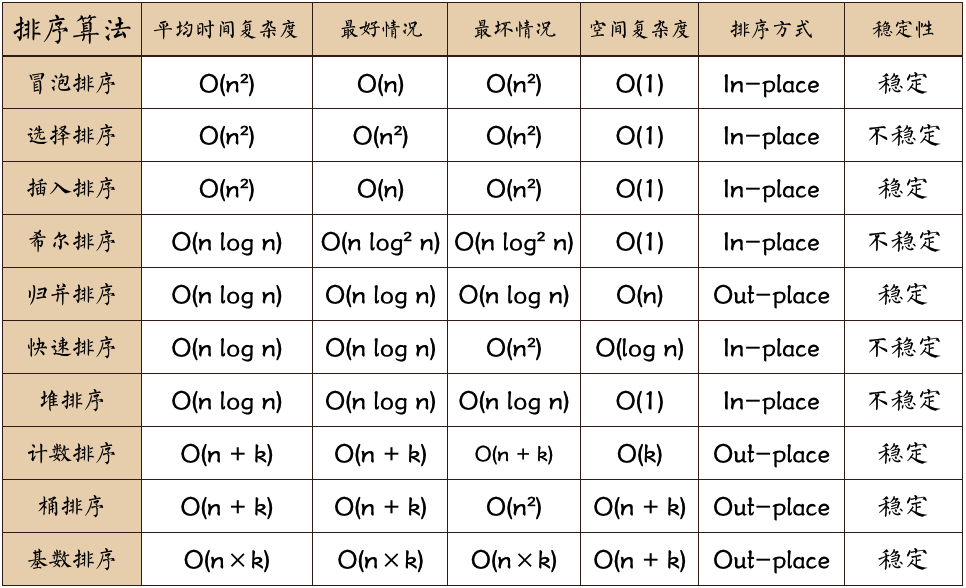
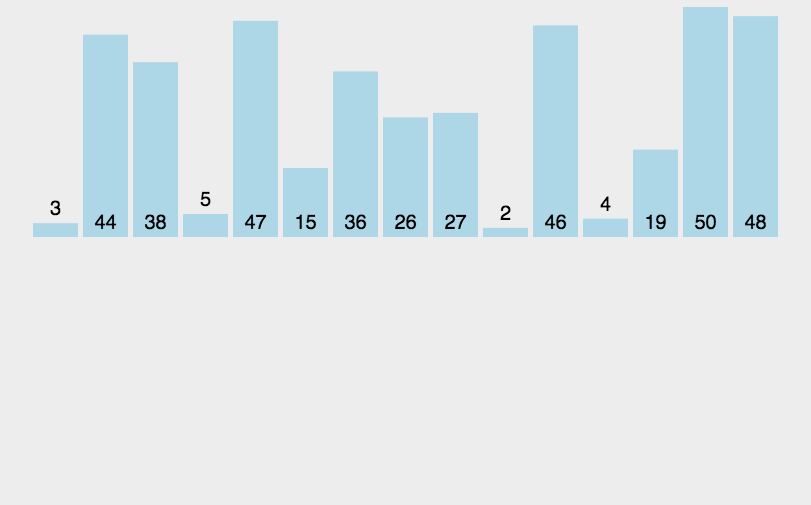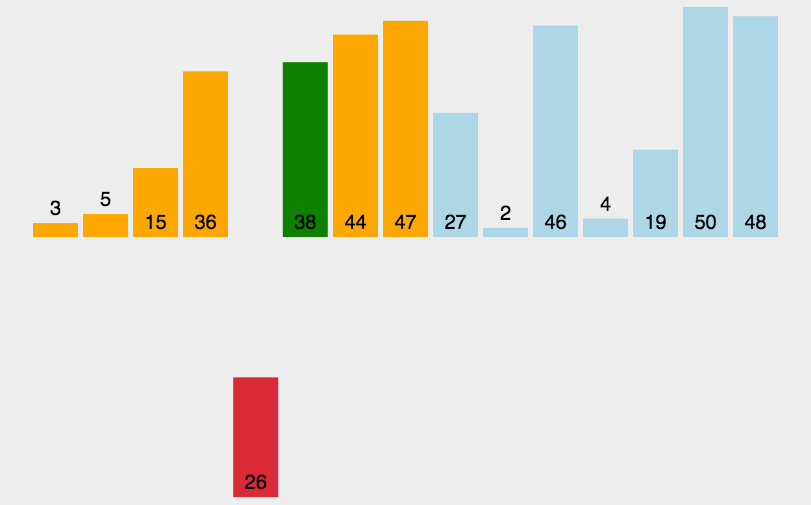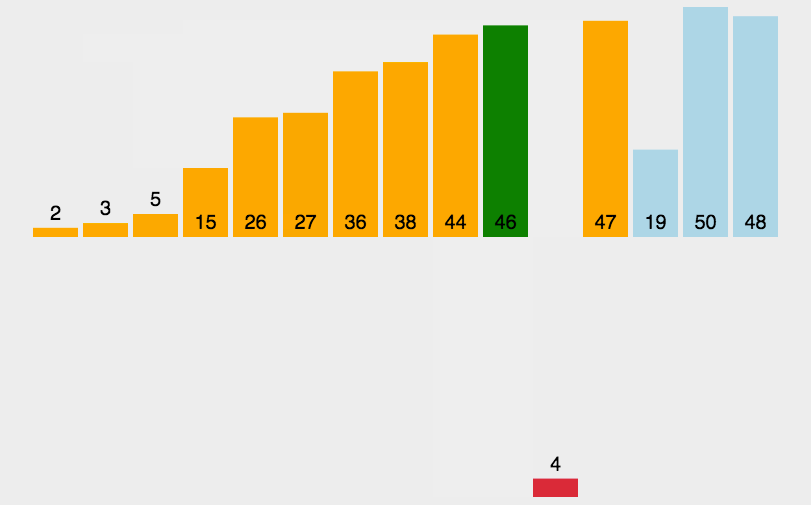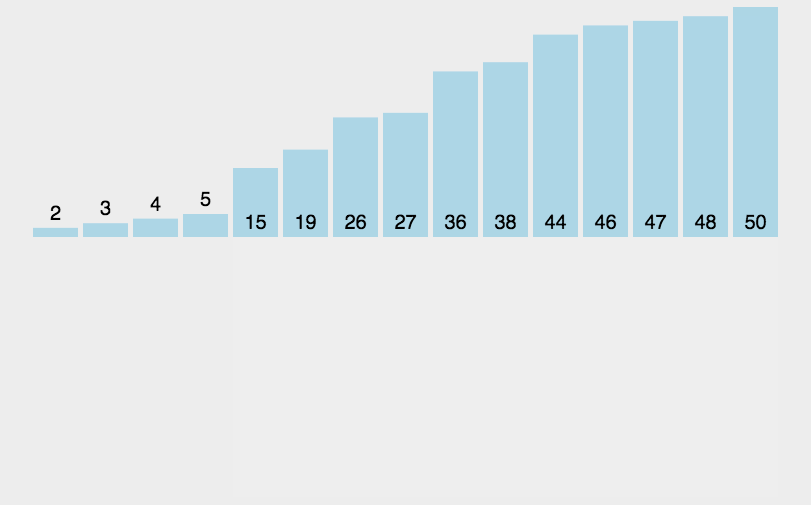
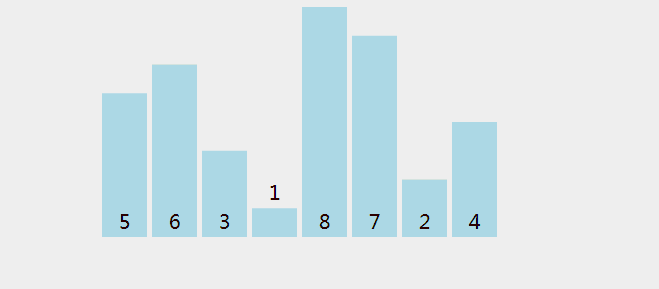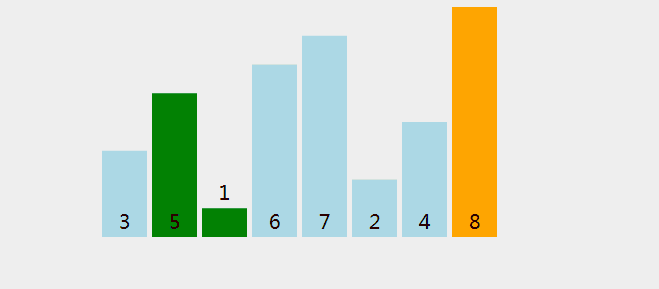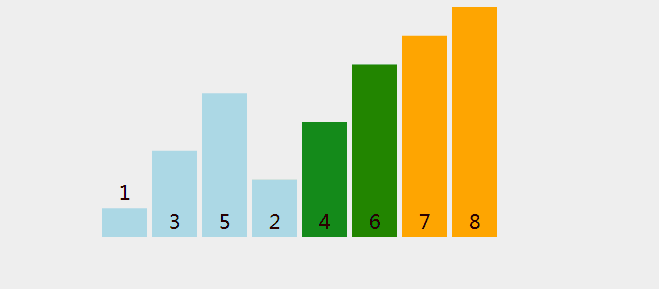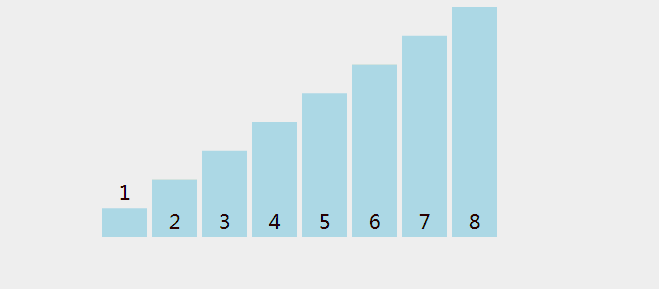冒泡排序：一种交换排序，它的基本思想是：两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。稳定排序算法

时间复杂度 O(n2)，里层循环每趟比较第 j 项和第 j+1项，如果前项大于后项，则发生交换。缺点是每次比较后都可能发生交换，交换次数太多了，值从小到大。

通俗概述：依次比较相邻两关键字，如果反序则立即发生交换，如果正序则继续比较下一个相邻项，双重嵌套循环实现

具体如何移动呢？我们先看一个例子

有8个数字组成一个无序数列{5,6,3,1,8,7,2,4},希望按照从小到大的顺序 对其进行排序。详细排序如下，第一轮排序结束，最大元素8冒泡排到最后。以此类推，下一轮7排序到倒数第二的位置…

实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class BubbleSort {
    // 利用双重循环，如果前一个数比后一个数大，则发生交换，每次比较都发生交换
    public static void sort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            for (int j = 1; j < arr.length - i; j++) {
                if (arr[j-1] > arr[j]) {
                    swap(arr, j-1, j);
                }
            }
        }
    }
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

选择排序

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class SelectionSort {

    public static void sort(int array[]){
        for (int i = 0; i < array.length; i++) {
            int minIndex = i; // 用来保存最小的索引,初始指向当前第i项
            for (int j = i; j < array.length; j++) {
                // 找到最小的数
                if (array[j] < array[minIndex]) {
                    //将最小数的索引保存
                    minIndex = j;
                }
            }
            // 交换元素。最小元素排在前边，依次递增
            int temp = array[minIndex];
            array[minIndex] = array[i];
            array[i] = temp;
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

插入排序

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。就像打扑克整理牌一样。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class InsertionSort {

    public static void sort(int[] arr) {
        // 第一个肯定是有序的，所以从第二个数开始遍历
        for (int i=1; i<arr.length; i++) {
            int current = arr[i]; // 取出第i个数，和前i-1个数比较，插入合适位置。
            int preIndex = i - 1; // 前一个数索引
            // 当发现小元素时，将已排序元素中所有大于它的后移一个单位
            while(preIndex >= 0 && arr[preIndex] > current) {
                arr[preIndex + 1] = arr[preIndex];
                preIndex--;
            }
            // 将目标元素插入到位移后留下的空位。最后一次交换结束后再自减运算，所以这里需要+1
            arr[preIndex + 1] = current;
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

快速排序

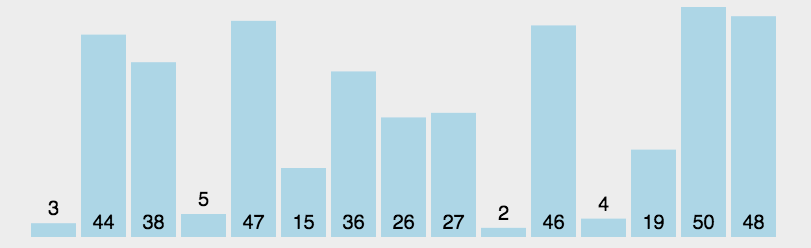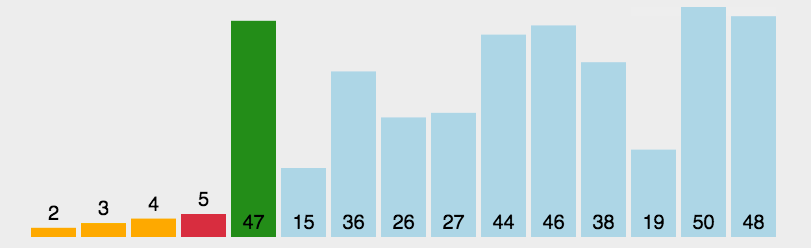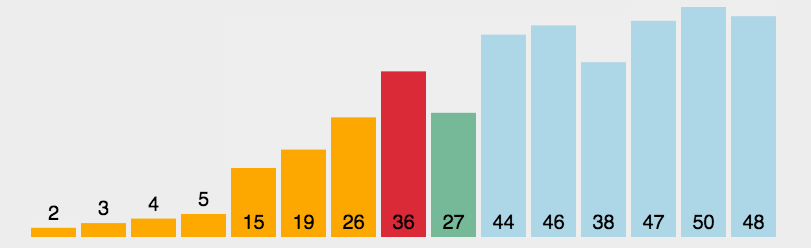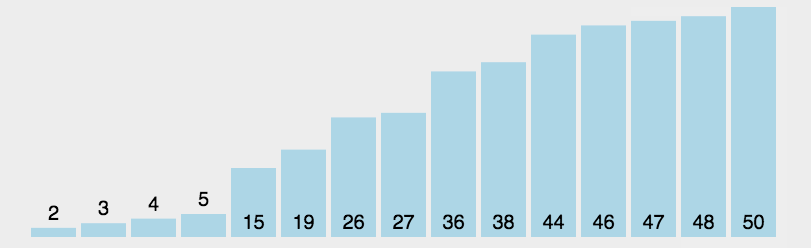
快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public class QuickSort {

    public static void sort(int[] arr, int startIndex, int endIndex) {
        // 递归结束条件: startIndex大于等于endIndex
        if (startIndex >= endIndex) {
            return;
        }
        //得到基准元素位置
        int pivotIndex = partition(arr, startIndex, endIndex);
        // 根据基准元素，分成2部分进行递归排序
        sort(arr, startIndex, pivotIndex-1);
        sort(arr, pivotIndex+1, endIndex);
    }

    // 分治(双边循环法)
    public static int partition(int[] arr, int startIndex, int endIndex) {
        // 取第一个位置的元素作为基准元素
        int pivot = arr[startIndex];
        int left = startIndex;
        int right = endIndex;

        while (left != right) {
            // 控制right指针比较并左移,找到第一个小于基准值的元素索引
            while (left < right && arr[right] > pivot) {
                right--;
            }
            // 控制left指针比较并右移, 找到第一个大于基准值的元素索引
            while (left < right && arr[left] <= pivot) {
                left++;
            }
            // 交换left和right指针所指向的元素
            if (left < right) {
                int temp = arr[left];
                arr[left] = arr[right];
                arr[right] = temp;
            }
        }

        // pivot和指针重合点交换
        arr[startIndex] = arr[left];
        arr[left] = pivot;

        return left;
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

总结快速排序的思想：冒泡+二分+递归分治

希尔排序

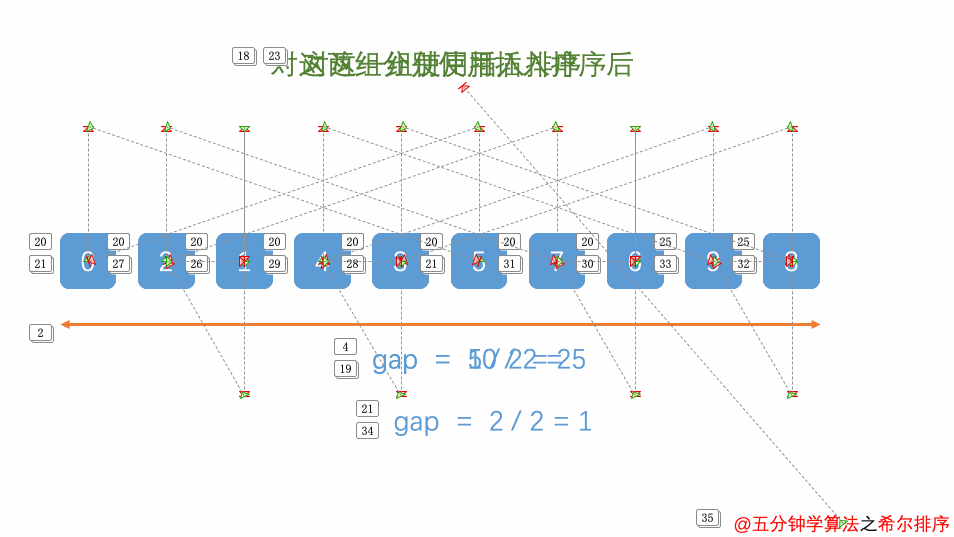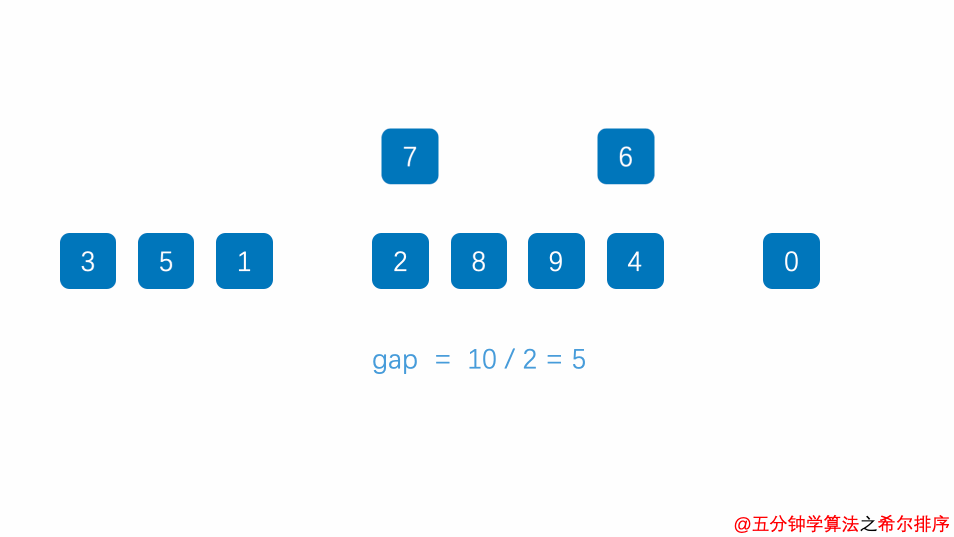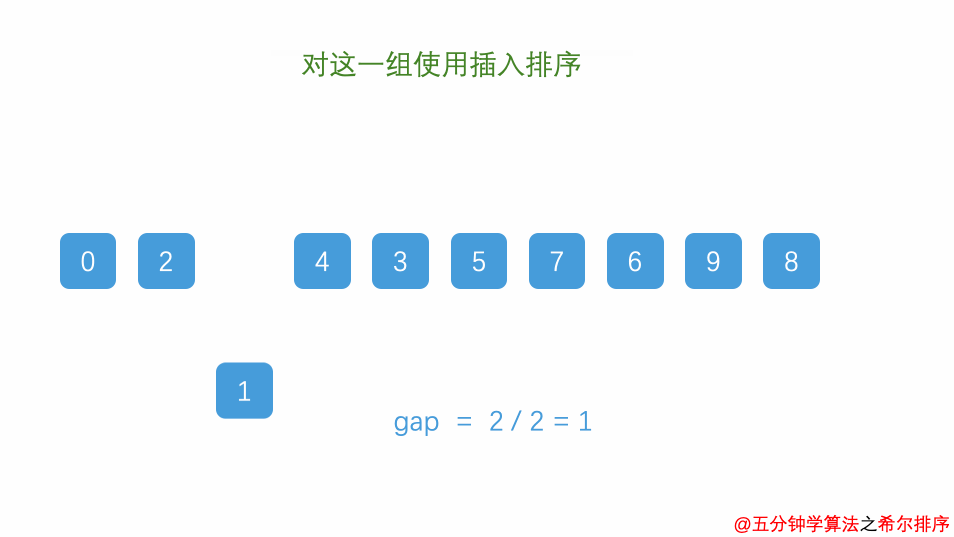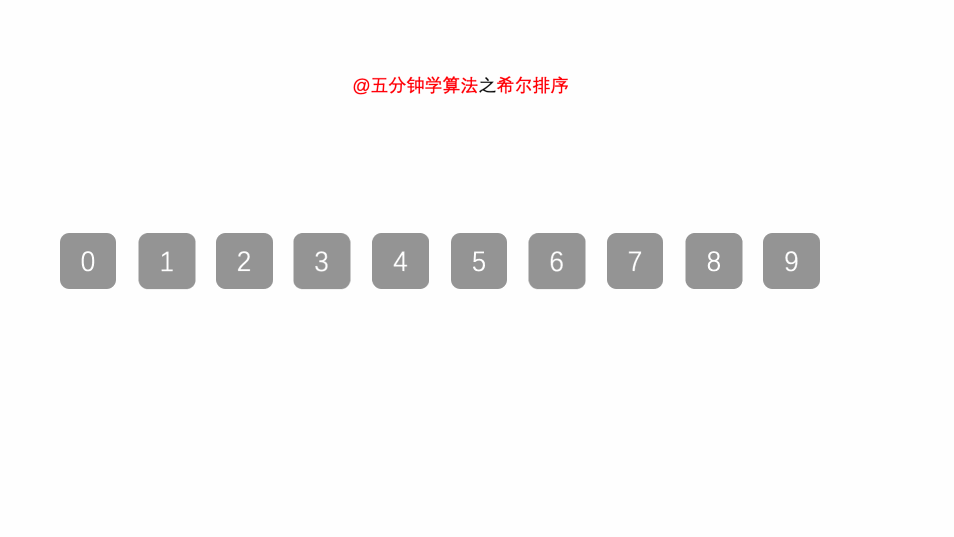
希尔排序：又称为增量排序，它是一种插入排序，它是直接插入排序算法的一种威力加强版。它的基本思想是：把记录按步长 gap(差距，间隙) 分组，对每组记录采用直接插入排序方法进行排序。 随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

时间复杂度为O(nlogn)，该方法因DL．Shell于1959年提出而得名。超越了O(n2)的算法的历史。他是在直接插入排序的增强，将记录按步长gap分组，然后在分组内进行直接插入排序。不稳定算法。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class ShellSort {

    public static void sort(int[] arr) {
        //初始化步长为数组长度的一半
        int gap = arr.length / 2;
        //循环结束条件，当gap<1是，循环结束，即排序结束
        while (gap >= 1) {
            //把距离为gap的元素编为一个组，扫描所有组
            for (int i = gap; i < arr.length; i++) {
                int current = arr[i];//保存待插入元素，以便组内元素向后移动覆盖
                int j = i;
                //对距离为gap的组内元素进行直接选择排序
                while (j-gap >=0 && current < arr[j-gap]) {
                    arr[j] = arr[j-gap];
                    j-=gap;
                }
                //将待插入元素插入合适位置
                arr[j] = current;
            }
            //一次循环结束，所有分组均已完成直接选择排序，则可将将距离缩小为原本的一半
            gap/=2;
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

堆排序

堆排序：就是利用堆进行排序的方法。它的基本思想是，将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根结点，将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的n-1给序列重新构造成一个堆，这样就会得到n个元素中的次小值。如此反复执行，便能得到一个有序序列。--------用直接插入排序，将数组调整为堆结构，然后再简单选择排序，选择最值交换，再调整堆结构。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
public class HeapSort {

    /**
     * 将数组调整为符合堆规律的结构
     * @param arr   传入需要调整的数组
     * @param parent    父结点
     * @param length    需要调整的数组长度
     */
    public static void heapAdjust(int[] arr, int parent, int length) {
        int temp = arr[parent];//先保存父结点的值，以便后续移动交换
        int child = parent * 2 + 1;//先获取到该父结点的左子结点
        while (child < length) {
            //如果存在右子结点，且右子结点大于左子结点，则选取右子结点
            if (child + 1 < length && arr[child] < arr[child + 1]) {
                child++;
            }
            //判断父结点（待插入的值）是否比子节点大
            if(temp>arr[child]){
                break;//父结点大，结束当前循环
            }else {
                /*此处类似与直接插入排序的思想*/
                arr[parent]=arr[child];//将子结点的值覆盖父节点的值
                parent=child;
                child=child *2+1;
            }
        }
        //此时已经找到合适的位置,将待插入的值插入合适的位置
        arr[parent]=temp;
    }

    /**
     *堆排序(升序)
     * @param list
     */
    public static void sort(int[] list){
        // 把无序数组构建成最大堆
        for (int i = list.length/2; i >=0 ; i--) {
            heapAdjust(list,i,list.length);
        }
        //循环删除堆顶元素
        for (int i = list.length-1; i >0; i--) {
            //将最大值list[0]与最后一个元素交换
            int temp=list[i];
            list[i]=list[0];
            list[0]=temp;
            //交换完之后，最大值已经在底层数组的末尾，然后将交换后的堆进行调整
            heapAdjust(list,0,i);//注意这里的长度已经-1了，所以堆调整不包含最后一个元素
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

归并排序

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class MergeSort {

    /**
     * 递归分治
     * @param arr
     * @param left
     * @param right
     */
    public static void sort(int[] arr, int left, int right) {
        if(left >= right)
        return ;
        int mid = (left + right) / 2;

        sort(arr, left, mid); //递归排序左边
        sort(arr, mid+1, right); //递归排序右边
        merge(arr, left, mid, right); //合并
    }

    /**
     * 合并两个有序数组
     * @param arr 待合并数组
     * @param left 左指针
     * @param mid 中间指针
     * @param right 右指针
     */
    public static void merge(int[] arr, int left, int mid, int right) {
        //[left, mid] [mid+1, right]
        int[] temp = new int[right - left + 1]; //中间数组

        int i = left;
        int j = mid + 1;
        int k = 0;
        while(i <= mid && j <= right) {
            if(arr[i] <= arr[j]) {
                temp[k++] = arr[i++];
            }
        else {
                temp[k++] = arr[j++];
            }
        }

        while(i <= mid) {
            temp[k++] = arr[i++];
        }

        while(j <= right) {
            temp[k++] = arr[j++];
        }

        for(int p=0; p<temp.length; p++) {
            arr[left + p] = temp[p];
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr,0, arr.length-1);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

计数排序

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

算法描述

  • 找出待排序的数组中最大和最小的元素；
  • 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
  • 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
  • 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class CountingSort {

    public static void sort(int[] arr) {
        //找出数组中的最大值
        int max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        //初始化计数数组
        int[] countArr = new int[max + 1];
        Arrays.fill(countArr, 0);

        //计数
        for (int i = 0; i < arr.length; i++) {
            countArr[arr[i]]++;
        }

        //排序
        int index = 0;
        for (int i = 0; i < countArr.length; i++) {
            for(int j=0; j< countArr[i]; j++) {
                arr[index++] = i;
            }
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

算法描述

  • 设置一个定量的数组当作空桶；
  • 遍历输入数据，并且把数据一个一个放到对应的桶里去；
  • 对每个不是空的桶进行排序；
  • 从不是空的桶里把排好序的数据拼接起来。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class BucketSort {
    public static void sort(int[] arr){
        //最大最小值
        int max = arr[0];
        int min = arr[0];
        int length = arr.length;

        for(int i=1; i<length; i++) {
            if(arr[i] > max) {
                max = arr[i];
            } else if(arr[i] < min) {
                min = arr[i];
            }
        }

        //最大值和最小值的差
        int diff = max - min;

        //桶列表
        ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>();
        for(int i = 0; i < length; i++){
            bucketList.add(new ArrayList<>());
        }

        //每个桶的存数区间
        float section = (float) diff / (float) (length - 1);

        //数据入桶
        for(int i = 0; i < length; i++){
            //当前数除以区间得出存放桶的位置 减1后得出桶的下标
            int num = (int) (arr[i] / section) - 1;
            if(num < 0){
                num = 0;
            }
            bucketList.get(num).add(arr[i]);
        }

        //桶内排序
        for(int i = 0; i < bucketList.size(); i++){
            //jdk的排序速度当然信得过
            Collections.sort(bucketList.get(i));
        }

        //写入原数组
        int index = 0;
        for(ArrayList<Integer> arrayList : bucketList){
            for(int value : arrayList){
                arr[index] = value;
                index++;
            }
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }
}

基数排序

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

算法描述

  • 取得数组中的最大数，并取得位数；
  • arr为原始数组，从最低位开始取每个位组成radix数组；
  • 对radix进行计数排序（利用计数排序适用于小范围数的特点）；

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class RadixSort {
    public static void sort(int[] arr){
        int length = arr.length;

        //最大值
        int max = arr[0];
        for(int i = 0;i < length;i++){
            if(arr[i] > max){
                max = arr[i];
            }
        }
        //当前排序位置
        int location = 1;

        //桶列表
        ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>();

        //长度为10 装入余数0-9的数据
        for(int i = 0; i < 10; i++){
            bucketList.add(new ArrayList());
        }

        while(true)
        {
            //判断是否排完
            int dd = (int)Math.pow(10, (location - 1));
            if(max < dd){
                break;
            }

            //数据入桶
            for(int i = 0; i < length; i++)
            {
                //计算余数 放入相应的桶
                int number = ((arr[i] / dd) % 10);
                bucketList.get(number).add(arr[i]);
            }

            //写回数组
            int nn = 0;
            for (int i=0;i<10;i++){
                int size = bucketList.get(i).size();
                for(int ii = 0;ii < size;ii ++){
                    arr[nn++] = bucketList.get(i).get(ii);
                }
                bucketList.get(i).clear();
            }
            location++;
        }
    }

    public static void main(String[] args) {
        int[] arr=new int[]{5,6,3,1,8,7,2,4};
        sort(arr);
        System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
    }

}

当我遇上你

勿在浮沙筑高楼